In my July 27 blog I have discussed the case for electoral reform in Canada. The case is based on the high proportion of ridings that are won with simple pluralities rather than outright majorities. A little bit of electoral mathematics can take this analysis a bit further and show how voter concentration (or dispersion) is related to the margin of winning a riding.
There is a useful measure of voter dispersion that I will use in the analysis here: entropy. Consider riding \(i\), where \(n_i\) parties compete for votes. Each party \(j\) receives \(v_{ij}\) votes, and thus a share of \(p_{ij}=v_{ij}/v_i\), where \(v_i=\sum_j v_{ij}\) is the total number of votes in a riding. Then the measure \[ E_i=\exp\left(-\sum_{j=1}^{n_i} p_{ij}\ln(p_{ij})\right) \] is the exponential of entropy for riding \(i\). The expression in the large round parenthesis is the conventional measure of entropy. Taking the exponential transforms entropy into the "effective number of parties" competing in a riding. Consider the case when all parties receive the same share of votes and thus \(p_{ij}=1/n_{i}\). Then it turns out that \(E_i = n_i\). This is the maximum that can be attained in any riding. The minimum is always 1, when one party gains all votes and all others receive none. In other words, \(E_i\in[1,n_i]\). The entropy measure adjusts for the relative size of support for parties in each riding. If one large party competes against two small parties, the "effective number of parties" competing may well turn out to be just 2, which implies that the race in this riding may only be a two-way race rather than a true three-way race. An alternative measure is the Herfindahl index, but this measure would need to be adjusted awkwardly by the number of competing parties in a given riding. Entropy is a simpler and more robust measure of concentration with a particularly appealing interpretation.
The diagram below shows the distribution of the effective number of parties across ridings in Canada's 2011 federal election. It turns out that the mean for the effective number of parties is 3.2. On average, we have three-way races in Canada, and in some we even have competitive four-way races. This voter dispersion is a challenge for first-past-the-post electoral systems, which work best when there are only two parties competing.
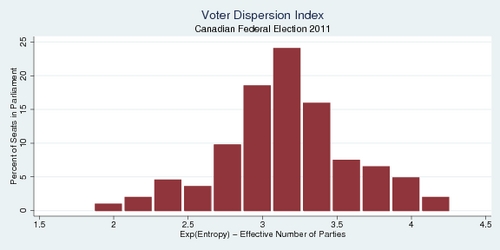
click on image for high-resolution PDF version
The voter dispersion identified above is a problem for our electoral system. How this voter dispersion correlates with the winning margin of the successful party is aggravating this problem. As the next diagram shows, there is negative correlation between the winning margin and the effective number of parties competing in a riding. The more parties compete, the more likely it is that the winning margin is very small. Another way to put this is that as you move from two-way races to three-way races, there is a tendency that the outcome of three-way races is more uncertain than for two-way races. Keep in mind that this is effect is not automatic. If you take a 60-40 split in a riding and replace it with a 60-20-20 split, the effective number of parties increases from 1.96 to 2.59, while the winning margin increases from 20% to 40%—this would be a positive correlation. What happens is more like moving from a 60-40 to a 40-35-25 split. The effective number of parties increases from 1.96 to 2.95, while the winning margin decreases from 20% to 5%—suggesting a negative correlation.
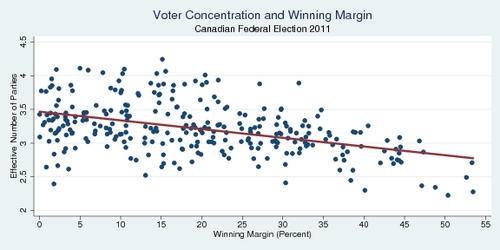
click on image for high-resolution PDF version
Voter dispersion and first-past-the-post electoral systems create problems for democratic "representativeness". In my July 27 blog I support hybrid systems that combine the benefits of majoritarian and proportional-representation systems.
One last question to look at involves the link between voter dispersion and participation. When there is more competition among parties, does voter participation go up? The diagram below gives the answer. There is a weak correlation; the data points scatter rather widely around the regression line. A greater number of parties competing raises participation marginally. But even though this effect is statistically significant, the effect on participation is rather weak. A larger number of competing parties does not raise participation much.
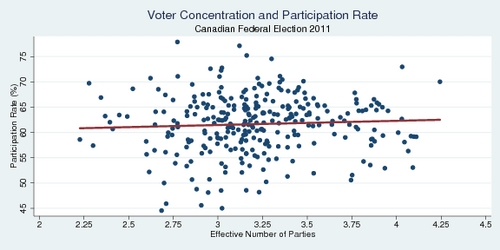
click on image for high-resolution PDF version
![[Sauder School of Business]](logo-ubc-sauder-2016.png)
![[The University of British Columbia]](logo-ubc-2016.png)