For a number of years B.C. Hydro has been offering electricity tariffs to businesses that promote energy conservation. The General Service Business Rates that are currently in effect promote energy conservation by using locally-high marginal costs, which is tantamount to a feebate system where increases in electricity consumption are punished with an extra fee and decreases in electricity use are rewarded with a rebate. Businesses pay both a capacity charge per kilowatt (kW) maximum use and an energy charge per kilowatthour (kWh) actual use. The energy charge is modified to provide an incentive, customized to each electricity user, to reduce consumption. Here is how it works, and how to make a cost-benefit analysis for investing into energy-saving devices.

B.C. Hydro calculates a baseline for each consumer for each month as a rolling average of the last three years of consumption. In the illustration below, the averages of May 2013, May 2014, and May 2015 are used to calculate the baseline for May 2016. In part 1 of the tariff, the customer is charged for the baseline consumption regardless of the actual level of electricity consumption. The part 1 tariff consists of a higher rate up to 14,800 kWh (Tier 1), and a lower rate for consumption over 14,800 kWh (Tier 2). For the medium-sized customer, the Tier 1 rate is currently $0.1030/kWh, and the Tier 2 rate is $0.0719/kWh.

click on image for high-resolution PDF version

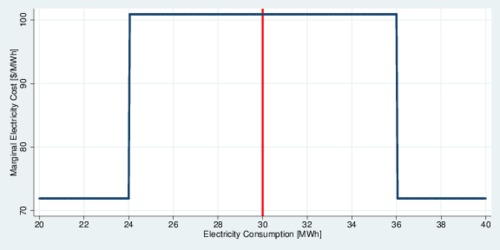
It gets more interesting in the next step. Let us assume that a customer has a baseline consumption of 30 MWh (i.e., 30,000 kWh), as shown by the red vertical line in the next diagram. B.C. Hydro now calculates a 20-percent band to each side, which ranges from 24 MWh to 36 MWh for a baseline of 30 MWh. The part 2 Tariff now sets a relatively high marginal rate of $0.1009/kWh for consumption exceeding the baseline and consumption below the baseline. A consumer who uses less than the baseline receives a rebate, while the consumer who uses more than the baseline pays a premium. As the diagram below shows, the marginal electricity rate—what you pay for the next kWh of consumption—jumps up from $71.90/MWh to $100.90/MWh when consumption falls within the 20-percent band around the baseline. What is the benefit of this jump in marginal rate?

click on image for high-resolution PDF version

Economic theory holds that consumers react to marginal rates. The energy conservation tariff locally raises the marginal rate, which means that the consumer should become more reactive to the price of electricity. Of course, if the electricity consumer does not change behaviour and consumption drifts randomly around the baseline, the locally-high marginal rate accomplishes nothing. However, the power-smart consumer will benefit if she invests in energy-saving equipment, and the higher marginal rate boosts the return on investment. Let us see how this calculation works.

Let us assume that a business has indeed a 30 MWh baseline of electricity use based on the last three years of consumption. The business has an opportunity to invest $25,000 into a new heating system that will permanently reduce energy consumption by 10%, a 3 MWh per month reduction from 30 MWh to 27 MWh. In the first twelve months of using this technology, the 10% reduction yields (12 months) times (3 MWh) times ($110.9/MWh) equal $3,992.40. In the second year, the baseline adjusts from 30 MWh to (30+30+27)/3 = 29 MWh. So in the second year, the company gains another $2,661.60. In the third year the baseline drops to (30+27+27)/3= 28 MWh, and the business gains another $1,330.80. The electricity rebate is thus twice the amount of the first year alone, so $7,984.80. But this is not all the money that is saved; this was just the rebate. In perpetuity, the business saves (12 months) times (3 MWh) times ($71.90/MWh)= $2,588.40 per year. And in years 2 and 3, the shift in the baseline saves $826.80 and $1,725.60, respectively. Now we simply need to add together all these savings, and calculate the present-discounted value. For that purpose, a bit of math helps along the way.

Let \(\tau_1\) denote the base tariff per kWh, and let \(\tau_2>\tau_1\) denote the conservation tariff per kWh. The electricity conservation that results from investing in equipment is valued at \(s\) MWh. Further let \(\rho\) denote the discount rate. Then, starting in year zero, the benefit is given by: \[ \mathcal{B}(\tau_1,\tau_2)=s\left[ \tau_2 +\frac{2\tau_2 +\tau_1}{1+\rho}+\frac{\tau_2+2\tau_1}{(1+\rho)^2} +\sum_{t=3}^\infty \frac{\tau_1}{(1+\rho)^t}\right] \] Simplifying this expression yields \[\mathcal{B}(\tau_1,\tau_2)=s\left[\frac{\tau_1(\rho^2+3\rho+3)+\tau_2(3\rho^3+8\rho^2+6\rho)}{3\rho(1+\rho)^2}\right]\] Compare that to the case where \(\tau=\tau_1=\tau_2\), and thus \[\mathcal{B}(\tau_1)=s\cdot\tau_1\cdot\left(\frac{1+\rho}{\rho}\right)\] Here, the gains are simply the present-discounted value of \(\tau_1 s\). As a rule of thumb, with an 8% discount rate, the present-value multiplier in the round parentheses is 13.5. Multiply the annual savings by that number, and you have the total benefit. With the electricity feebate the savings are larger. We can further calculate the ratio of the two benefits: \[\mathcal{C}\equiv\frac{\mathcal{B}(\tau_1,\tau_2)}{\mathcal{B}(\tau_1)}= \frac{\rho^2+3\rho+3}{3(1+\rho)^3}+\frac{3\rho^3+8\rho^2+6\rho}{3(1+\rho)^3}\left(\frac{\tau_2}{\tau_1}\right)\] which turns out to be a function of the ratio \(\tau_2/\tau_1\) and is independent of \(s\). We can use the actual ratio $100.90/$71.90=1.4033 and a discount rate of 5% to calculate the increase in benefits. It turns out to be a 3.7% increase in benefits. If the discount rate was higher, say 10%, then the gains would increase to 6.9%. Essentially, the utility "subsidizes" the installation of energy efficiency devices at a rate of roughly 4-7%.

Returning to our business, the 3 MWh energy conservation per month equals \(s=36\) MWh per year. We allow for a discount rate of 8%, considering that a commercial entity has higher profit expectations than a household. Thus, \(\mathcal{B}=\) $36,930. This means that an investment of $25,000 will pay off: the benefits exceed the cost. You may wonder if a $25,000 investment is a realistic figure. The 3 MWh per month is equal to a constant load of 4.167 kW (=3,000 kWh divided by 720 hours per month). This means the capital cost calculates as $6,000/kW. If you compare that to capital costs reported by the US Energy Information Administration in Updated Capital Cost Estimates for Utility Scale Electricity Generating Plants, April 2013, the number is roughly in the ballpark for new generation capacity (once you allow for the USD exchange rate).

The utility's problem is to figure out the optimal ratio \(\tau_2/\tau_1\). This depends crucially on the the capital cost of bringing new generation capacity online. It would not make sense to pay much more for energy conservation than for providing new capacity. In other words, the ratio \(\mathcal{C}\) above should not exceed the ratio of new generation cost to average generation cost; let us call that generation cost ratio \(\phi>1\). If we continue assuming a discount rate of 8%, then we can solve the equation above for the ratio of \(\tau_2/\tau_1\) as follows: \[\tau_2/\tau_1\approx 7.0938\cdot\phi-6.0938\] So if the new generation cost is 20% higher than the average cost, then \(\phi=1.20\) and thus \(\tau_2/\tau_1=2.42\). The energy conservation tariff \(\tau_2\) can be up to 2.42 as high as the base tariff \(\tau_1\). Unfortunately, I do not know B.C. Hydro's ratio of new-to-old generation cost \(\phi\), and of course one can argue the size of the discount rate. However, my sense is that B.C. Hydro has still room left to increase the \(\tau_2/\tau_1\) ratio to make the energy conservation tariff more effective. This said, I applaud B.C. Hydro for using marginal cost pricing to incentivize energy conservation. This tool is particularly effective for businesses because: (i) they are more likely than households to overcome information problems (figuring out costs and benefits for energy conservation investments); (ii) the discount rate for businesses is generally assumed to be higher than for individuals; (iii) the electricity use profile of businesses tends to be much "flatter" than for households, which means that deviations from the baseline are more likely the result of business decisions than random "noise".

The remaining question is a research question: is there empirical evidence that energy conservation tariffs deliver the intended reductions in electricity use? If I had the data from B.C. Hydro, I would love to look into it.

Perhaps the biggest challenge with energy conservation tariffs is overcoming the information problem. Do businesses understand how this system works? Do they pay attention? Perhaps we need more energy consultants advising businesses on opportunities to save money through smart investments in energy conservation.