When governments increase taxes on a product, how much gets passed on to consumers? This is the question about the incidence of taxation. Whenever a new tax is introduced or raised, or an import tariff is raised or lowered, we wonder about how much of this change will be passed on to consumers. Especially the recent US tariffs imposed on Canadian and Chinese exports, as well as retaliatory tariffs imposed on US exports, raise the question about who will bear most of the burden: consumers or producers. The answer depends crucially on the market structure and the price elasticity of demand. The range of outcomes can vary greatly. Let's have a look at the conventional wisdom on tax pass-through, which applies to highly competitive markets, as well as some newer work on how this pass-through changes when markets are monopolistic or oligopolistic. This topic was inspired by a recent research seminar by my UCLA colleague Brett Hollenbeck, who presented his work on taxation and market power in the legal marijuana industry in Washington state. For goods such as alcohol, tobacco, and (soon to be legal in Canada) cannabis, tax rates can be quite high. Take wine in British Columbia, for example. The wholesale mark-up is 89%, and then on top of that is still 10% PST and 5% GST, so the overall tax rate can be as high as 117%. So what does economic theory tell us about the pass-through and distribution of burden?

There is one important distinction that needs to be made. Local incidence describes what happens when a tax is raised at the margin: how is the next dollar of taxation split between consumers and producers? By comparison, the global incidence of taxation is about the division of the overall tax burden between consumers and producers. Whenever taxes are imposed, there is also a dead-weight loss (DWL) due to decreased efficiency. This DWL is ignored when we merely want to know which share consumers and producers carry of the direct tax burden. However, when we are interested in the total tax burden, quantifying the dead-weight loss is important as we are interested in the total change in consumer surplus and producer surplus.

General Model

Under perfect competition, the pass-through rate is determined by the price elasticity of supply \(\eta_S\) and the (positive) price elasticity of demand \(\eta_D\) so that the pass-through rate is \[\rho=\frac{1}{1+\eta_D/\eta_S}\] If demand is perfectly elastic and \(\eta_D\rightarrow\infty\), then \(\rho\rightarrow0\) implies that producers bear the full burden. The reverse is true when demand is perfectly inelastic and consumers end up with the tax burden. When supply is perfectly elastic and \(\eta_S\rightarrow\infty\), then \(\rho\rightarrow1\) and producers end up with the tax burden. So the general rule is that parties with inelastic supply or demand bear taxes, and parties with elastic supply or demand avoid them.

Monopolistic Market

It is quite informative to also look at the case of a monopolistic market. A rigorous economic analysis can be found in Weyl and Fabinger (2013). The analysis can be simplified a bit by relying on a specific demand model. Let us assume that a monopolistic producer has a marginal cost \(c\) and faces negative exponential demand \[Q=a\cdot\exp(-p^\circ/b)\] where \(a\) is a measure of the market size (measured in units of goods), \(b\) is the unit-elasticity price (measured in $/unit), and \(p^\circ\) is the after-tax price that consumers pay. I had discussed the virtues of negative exponential demand in a previous blog this June. Assume that a tax is imposed as a percentage so that the market price is \(p^\circ=(1+\tau)p\), where \(p\) is the producer price net of taxes. The monopolist maximizes profits \[\pi=(p-c)\cdot Q(p^\circ)=(p-c)\cdot Q((1+\tau)p)\] so that the first-order condition for a maximum yields the optimal producer price and after-tax price \[p^\ast=c+\frac{b}{1+\tau} \quad\Longrightarrow\quad p^\circ=b+c\cdot(1+\tau)\] It is useful to introduce the mark-up \(\psi\equiv(p-c)/c=b/c\), which in the case of negative exponential demand is simply the ratio of unit-elasticity price and marginal cost.

We can calculate the marginal pass-through rate s \[\rho=\frac{\mathrm{d}p^\circ}{\mathrm{d}\tau}\frac{\tau}{p^\circ}= \frac{1}{1+(1+\psi)/\tau}\] If the tax rate is small initially, the pass-through rate remains low regardless of the mark-up (blue areas). However, when mark-ups are low, additional taxes shift the burden quickly to the consumers (yellow and red areas). The "heat map" diagram below shows how the pass-through varies both with the tax rate and the pre-tax mark-up. The tax pass-through is small only when tax rates are low.

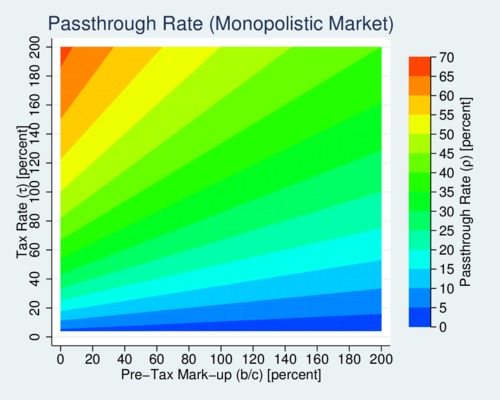
click on image for high resolution PDF veresion

The next diagram focuses on the overall (global incidence) of the tax burden, and this looks a bit different from the (local incidence) of additional tax burden. Ignoring the inefficiency (dead-weight) loss from imposing the tax, the share of tax that is borne by consumers is \[\chi=\frac{1}{1+\psi/(1+\tau)}\] This value is calculated by comparing the difference between the after-tax and before-tax price for consumers, equal to \(\tau c\), relative to the total tax wedge, equal to \(\tau(c+b/(1+\tau)\). This expression looks very similar to that for \(\rho\), but the "average" tax burden looks quite different from the "marginal" tax burden. When mark-ups are low, consumers carry nearly all of the burden regardless of the tax rate. The blue areas where the consumer burden is less than 50% require the monopolist to start off with very high pre-tax mark-ups, while taxes need to remain relatively low. Most of the time consumers will absorb the lion's share of the tax burden.

The example here shows a minor additional insight to the conventional treatment of tax incidence in textbooks. The allocation of the tax burden depends on the mark-up as well as the tax level. These two variables interact in practice. The higher the tax rate, the more tax burden is carried by consumers.

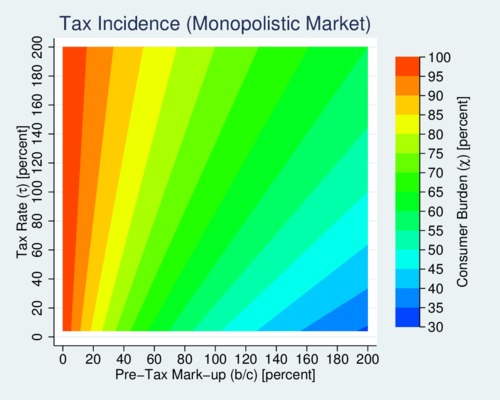
click on image for high resolution PDF veresion

Oligopolistic Markets

When markets are oligopolistic, assume that producers compete on quantity and choose that quantity independently of each other. Then the market price that emerges (derived in my previous blog) is given by \(p=\bar{c}+b/(1+\tau)/n\), where \(n\) is the number of firms and \(\bar{c}\) is the average production cost. So the main difference is that the unit-price elasticity \(b\) is divided by the number of firms. This means that unlike the monopolist, oligopolistic producers can operate on the inelastic part of the demand curve. Compared to the monopolistic case, we are now dealing with "average mark-ups" instead of a single-producer mark-up. Oligopolistic mark-ups are lower than monopolistic mark-ups because more firms compete. In the diagram above we will therefore stick to the left of the diagram where mark-ups are low. This means that the tax burden will be borne mostly by consumers.

Takeaways

Pass-through rates and tax burdens differ hugely depending on the market structure, demand characteristics, as well as the level of taxation. While the simple model that characterizes "local incidence" is usually a good start, the total welfare implications require information about demand and market structure. The second heat map diagram gives a good idea about relating mark-ups and tax rates to the share of tax burden borne by consumers. Monopolistic markets are not making consumers better off when taxes go up except in rare circumstances when producers already benefit from abnormally high mark-ups. Monopolists will only share their pie when the pie has lots of icing. Market structure mattes as well. The more competitive the market, the more consumers will carry the burden of higher taxes. But that is little consolation when tax incidence for consumers is already high when the market structure is completely monopolistic.

When Canada legalizes marijuana on October 17, 2018, initial mark-ups may be high while the tax rate remains somewhat low. There is reason to think that at least initially the tax burden will be shared roughly equally between producers and consumers. However, as competition heats up and mark-ups decline, the tax burden will fall more and more on consumers.